Confidence Intervals for Sample Size Less Than 30

In the preceding word we have been using southward, the population standard divergence, to compute the standard error. However, nosotros don't really know the population standard deviation, since we are working from samples. To get around this, nosotros have been using the sample standard deviation (s) as an estimate. This is not a trouble if the sample size is xxx or greater because of the fundamental limit theorem. Nevertheless, if the sample is minor (<30) , we have to conform and use a t-value instead of a Z score in order to account for the smaller sample size and using the sample SD.

Therefore, if n<30, use the appropriate t score instead of a z score, and note that the t-value will depend on the degrees of freedom (df) as a reflection of sample size. When using the t-distribution to compute a confidence interval, df = n-one.

Adding of a 95% confidence interval when n<30 will then employ the advisable t-value in place of Z in the formula:

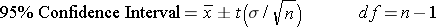
The T-distribution

One fashion to call back about the t-distribution is that it is actually a large family unit of distributions that are similar in shape to the normal standard distribution, just adapted to account for smaller sample sizes. A t-distribution for a small sample size would look like a squashed down version of the standard normal distribution, but every bit the sample size increment the t-distribution volition become closer and closer to approximating the standard normal distribution.

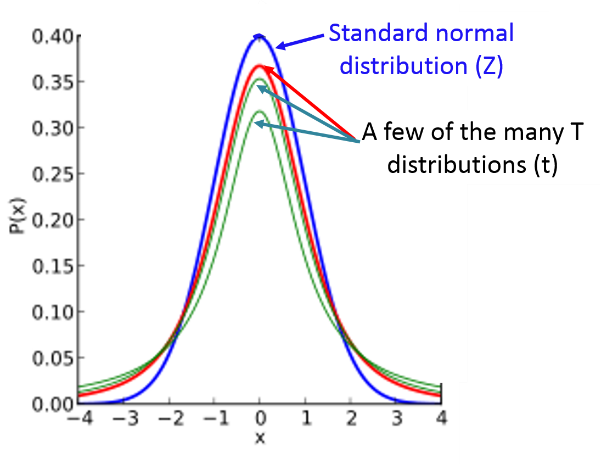
The tabular array below shows a portion of the table for the t-distribution. Notice that sample size is represented past the "degrees of liberty" in the offset column. For determining the conviction interval df=due north-1. Notice besides that this tabular array is ready a lot differently than the table of Z scores. Hither, but five levels of probability are shown in the column titles, whereas in the tabular array of Z scores, the probabilities were in the interior of the table. Consequently, the levels of probability are much more limited here, considering t-values depend on the degrees of freedom, which are listed in the rows.

Conviction Level

fourscore%

90%

95%

98%

99%

2-sided test p-values

.20

.10

.05

.02

.01

One-sided test p-values

.10

.05

.025

.01

.005

Degrees of Freedom (df)

1

3.078

six.314

12.71

31.82

63.66

2

1.886

2.920

iv.303

6.965

nine.925

iii

1.638

2.353

3.182

4.541

five.841

4

ane.533

2.132

2.776

3.747

iv.604

5

one.476

2.015

ii.571

3.365

4.032

6

1.440

1.943

two.447

3.143

3.707

7

1.415

1.895

2.365

2.998

iii.499

8

1.397

1.860

2.306

two.896

3.355

nine

1.383

1.833

2.262

ii.821

3.250

10

1.372

1.812

2.228

2.764

3.169

11

1.362

1.796

ii.201

ii.718

3.106

12

1.356

1.782

2.179

2.681

3.055

xiii

1.350

one.771

two.160

2.650

three.012

14

1.345

i.761

2.145

two.624

ii.977

15

1.341

1.753

2.131

two.602

2.947

16

1.337

1.746

2.120

2.583

2.921

17

one.333

ane.740

2.110

2.567

two.898

18

1.330

1.734

2.101

2.552

2.878

19

1.328

1.729

2.093

2.539

2.861

twenty

1.325

1.725

2.086

2.528

2.845

Notice that the value of t is larger for smaller sample sizes (i.e., lower df). When nosotros use "t" instead of "Z" in the equation for the confidence interval, it will result in a larger margin of fault and a wider confidence interval reflecting the smaller sample size.

With an infinitely large sample size the t-distribution and the standard normal distribution volition be the aforementioned, and for samples greater than 30 they will be like, merely the t-distribution will be somewhat more than conservative. Consequently, one can ever employ a t-distribution instead of the standard normal distribution. However, when yous want to compute a 95% confidence interval for an guess from a large sample, it is easier to just use Z=1.96.

Because the t-distribution is, if anything, more than conservative, R relies heavily on the t-distribution.

Exam Yourself

Problem #one

Using the table above, what is the critical t score for a 95% confidence interval if the sample size (n) is 11?

Answer

Problem #2

A sample of northward=10 patients free of diabetes have their body mass index (BMI) measured. The mean is 27.26 with a standard difference of 2.10. Generate a ninety% confidence interval for the mean BMI amidst patients complimentary of diabetes.

Link to Respond in a Word file

Confidence Intervals for a Mean Using R

Instead of using the table, you lot can use R to generate t-values. For example, to generate t values for computing a 95% conviction interval, employ the function qt(i-tail area,df).

For case, if the sample size is 15, then df=14, we can calculate the t-score for the lower and upper tails of the 95% confidence interval in R:

> qt(0.025,fourteen)
[1] -2.144787
> qt(0.975,14 )
[1] 2.144787

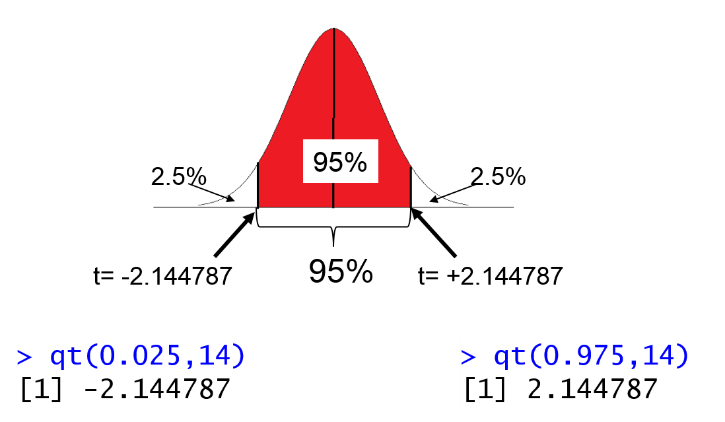
Then, to compute the 95% confidence interval we could plug t=2.144787 into the equation:

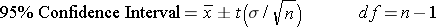
Confidence Intervals from Raw Information Using R

It is too easy to compute the point gauge and 95% conviction interval from a raw data prepare using the " t.test " function in R. For example, in the data prepare from the Weymouth Wellness Survey I could compute the mean and 95% conviction interval for BMI equally follows. First, I would load the data set and give it a short nickname. So I would attach the data fix, and then use the post-obit command:

> t.test(bmi)

The output would look like this:

1 Sample t-test

information:  bmi
t = 228.5395, df = 3231, p-value < ii.2e-16
alternative hypothesis: true hateful is non equal to 0
95 percent confidence interval:
26.66357 27.12504
sample estimates:
hateful of ten
26.8943

R defaults to calculating a 95% conviction interval, but you can specify the conviction interval as follows:

> t.test(bmi,conf.level=.90)

This would compute a xc% confidence interval.

Test Yourself

Lozoff and colleagues compared developmental outcomes in children who had been anemic in infancy to those in children who had not been anemic. Some of the data are shown in the tabular array below.

Mean + SD

Anemia in Infancy

(north=thirty)

Non-anemic in Infancy

(northward=133)

Gross Motor Score

52.four+xiv.3

58.7+12.5

Verbal IQ

101.4+xiii.two`

102.9+12.four

Source: Lozoff et al.: Long-term Developmental Issue of Infants with Iron Deficiency, NEJM, 1991

Compute the 95% conviction interval for verbal IQ using the t-distribution

Link to the Respond in a Word file

render to top | previous page | next page